TABLA DE CONVERSIONES
Longitud
1 Milla
|
=
|
1,609.3 mts
|
1 Kilómetro
|
=
|
1,000 mts
|
1 Metro
|
=
= = |
100 cms
1.0936 Yardas 3.28 Pies |
1 Yardas
|
=
|
3,0 Pies
|
1 Pie
|
=
= |
12 Pulgadas
30.48 cms |
1 Pulgada
|
=
|
2.54 cms
|
Volumen
1 mt 3
|
=
= |
1,000 dm3
1,000 Litros |
1 dm 3
|
=
= |
1 Litro
1,000 cms3 |
1 Galón
|
=
= |
8 Pintas
4.5461 Litros |
Superficie
1 Km. 2
|
=
|
100 Hectáreas
|
1 Hectárea
|
=
= |
10,000 mts2
2.471 Acres |
1 Acre
|
=
|
4,046.9 mts2
|
1 m2
|
=
|
10,000 cm2
|
1 cm2
|
=
|
100 mm2
|
Peso
1 Tonelada
|
=
|
1,000 Kgs.
|
1 Quintal
|
=
|
100 Kgs.
|
1 Quintal Z
|
=
|
100 Libras
|
1 Kilo
|
=
= |
1,000 grs.
2.2046 Libras |
1 Libra
|
=
= |
453.597 grs.
16 Onzas |
1 Gramo
|
=
|
1,000 mgs.
|
1 Onza
|
=
|
28.349 grs
|
1 Quilate
|
=
|
205 mgs.
|
1 Arroba
|
=
= |
11.502 Kgs.
25 Libras |
Temperatura
| C | F | |
| -17.77 | = | 0 |
| 0 | = | 32 |
| 5 | = | 41 |
| 10 | = | 50 |
| 15 | = | 59 |
| 18 | = | 64.4 |
| 20 | = | 68 |
| 21 | = | 69.8 |
| 22 | = | 71.6 |
| 23 | = | 73.4 |
| 24 | = | 75.2 |
| 25 | = | 77 |
| 30 | = | 86 |
| 32 | = | 89.6 |
| 35 | = | 95 |
| 37 | = | 98.6 |
| 40 | = | 104 |
| 50 | = | 122 |
| 60 | = | 140 |
| 70 | = | 158 |
| 100 | = | 212 |
° C/5 = ( ° F – 32 ) / 9
[( 9/5 ) ° C ] + 32 = ° F
Fuerza
1 onza = 28,349 gramos
1 libra = 453,592 gramos
1 Newton = 105 dinas = 0,2248 libras
1libra = 4,448 N
1 tonelada = 2000 libras
Potencia
1 watt (W) = 1 J/s
1 Ergio/s = 0,0000001 watt
1 HP = 0,746 kilowatt (KW)
Unidades de Masa
1 Tonelada = 1000 Kg
1 Quintal = 100 Kg
1 Gramo = 0,001 Kg
Unidades de Tiempo
Minuto (mn) = 60 s
Hora (h) = 3600 s
Dia (d) = 86400 s
Ejemplos
1) Convierta 360 Onzas A Toneladas
360 Onzas* 1 Tone. = 0.01 Toneladas
32,000 Onzas
2) Convierta 36 cm a Pies
36 Cm * 1 Pie = 1.18 Pies
30.48 cm
3) Convierta 60 Km/Horas a Mt/Seg.
60 km/h * 1000 mt * 1 h = 16.66 mt/seg
1 km 3600 seg
4) Convierta 6 Lt a Cm Cubico
6 lt * 1000 cm3 = 6000 cm3
1 lt
5) Convierta 30 @ a lbr
30@ * 25 lbr = 2,500 lbrs
1@
Movimiento rectilíneo uniforme
El movimiento rectilíneo uniforme (MRU) fue definido, por primera vez, por Galileo en los siguientes términos: "Por movimiento igual o uniforme entiendo aquél en el que los espacios recorridos por un móvil en tiempos iguales, tómense como se tomen, resultan iguales entre sí", o, dicho de otro modo, es un movimiento de velocidad v constante.
El MRU se caracteriza por:
a) Movimiento que se realiza en una sola dirección en el eje horizontal.
b) Velocidad constante; implica magnitud, sentido y dirección inalterables.
c) La magnitud de la velocidad recibe el nombre de rapidez. Este movimiento no presenta aceleración (aceleración = 0).
 |
| Rapidez fantástica. |
Concepto de rapidez y de velocidad
Muy fáciles de confundir, son usados a menudo como equivalentes para referirse a uno u otro.
Pero la rapidez (r) representa un valor numérico, una magnitud; por ejemplo, 30 km/h.
En cambio la velocidad representa un vector que incluye un valor numérico (30 Km/h) y que además posee un sentido y una dirección.
Cuando hablemos de rapidez habrá dos elementos muy importantes que considerar: la distancia (d) y el tiempo (t), íntimamente relacionados.
Así:
Si dos móviles demoran el mismo tiempo en recorrer distancias distintas, tiene mayor rapidez aquel que recorre la mayor de ellas.
Si dos móviles recorren la misma distancia en tiempos distintos, tiene mayor rapidez aquel que lo hace en menor tiempo.
Significado físico de la rapidez
La rapidez se calcula o se expresa en relación a la distancia recorrida en cierta unidad de tiempo y su fórmula general es la siguiente:
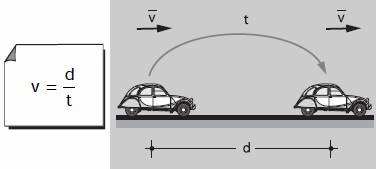 |
Donde
v = rapidez d = distancia o desplazamiento t = tiempo
|
Usamos v para representar la rapidez, la cual es igual al cociente entre la distancia (d) recorrida y el tiempo (t) empleado para hacerlo.
Formulas
V= S
T
T= S
V
S= V * T
S: Es la Distancia
V: Es la Velocidad
T: Es el Tiempo
EJEMPLOS
Con respecto a la fórmula usada para resolver los problemas de MRU diremos que es una sola.
V = D/T (Velocidad igual a distancia sobre tiempo).
Es decir que es una la ecuación que describe este movimiento. Otra utilizada para estos casos es la ecuación de posición (X).
X = Xi + V . T
X = Posición final
Xi = Posición inicial
Ejemplo: Calcula la posición final de un móvil que parte a 10 metros del origen con una velocidad igual a 45 Km/h durante 5 segundos.
En el apartado de pasaje de unidades describimos como se hacen los pasajes de velocidad de una unidad a otra. 45 Km/h equivalen a 12.5 mts/seg. Entonces:
X = 10 mts + 12.5 mts/seg. 5seg
X = 72.5 mts.
Volviendo a la primera fórmula veremos algunos ejemplos prácticos
Calcula la velocidad de un móvil que recorre 230 kms en 1.8 hs
V = D / t
V = 230 kms / 1.8 hs
V = 127.78 Kms/h
Calcula la distancia que recorre un atleta que corre a una velocidad de 9 mts/seg durante 16 segundos.
Despejamos la distancia de la fórmula V = d / t
D = V x t
D = 9 mts / seg x 16 seg
D = 144 mts.
En cuanto tiempo un vehículo recorrerá un tramo de 68 km si marcha a una velocidad de 82 Km/h.
T = D / V
T = 68 km / 82 Km/h
T = 0.83 hs.
Como no es un número muy adecuado para expresar la hora la pasamos a minutos
0,83 hs = 49 min y 45 seg (Ver pasaje de unidades)
Para finalizar veremos los gráficos que describen a este movimiento.
Distancia versus tiempo. La gráfica es una recta.
Velocidad versus tiempo. En este caso como la velocidad no varía, se representa con una línea paralela y recta. No tiene pendiente porque no varía.
GALILEO GALILEI
Galileo Galilei (Pisa, 15 de febrero de 15644 – Arcetri, 8 de enero de 1642)1 5 fue un astrónomo, filósofo, matemático y físico italiano que estuvo relacionado estrechamente con la revolución científica. Eminente hombre del Renacimiento, mostró interés por casi todas las ciencias y artes(música, literatura, pintura). Sus logros incluyen la mejora del telescopio, gran variedad de observaciones astronómicas, la primera ley del movimiento y un apoyo determinante para el copernicanismo. Ha sido considerado como el «padre de la astronomía moderna», el «padre de la física moderna»6 y el «padre de la ciencia».
Su trabajo experimental es considerado complementario a los escritos de Francis Bacon en el establecimiento del moderno método científico y su carrera científica es complementaria a la de Johannes Kepler. Su trabajo se considera una ruptura de las teorías asentadas de la física aristotélicay su enfrentamiento con la Inquisición romana de la Iglesia católica suele presentarse como el mejor ejemplo de conflicto entre religión y cienciaen la sociedad occidental.
Invención del telescopio
En mayo de 1609, Galileo recibe de París una carta del francés Jacques Badovere, uno de sus antiguos alumnos, quien le confirma un rumor insistente: la existencia de un telescopio que permite ver los objetos lejanos.14 Fabricado en Holanda, este telescopio habría permitido ya ver estrellas invisibles a simple vista. Con esta única descripción, Galileo, que ya no da cursos a Cosme II de Médicis, construye su primer telescopio. Al contrario que el telescopio holandés, éste no deforma los objetos y los aumenta 6 veces, o sea el doble que su oponente. También es el único de la época que consigue obtener una imagen derecha gracias a la utilización de una lente divergente en el ocular.[cita requerida] Este invento marca un giro en la vida de Galileo.
El 21 de agosto, apenas terminado su segundo telescopio (aumenta ocho o nueve veces), lo presenta al Senado de Venecia. La demostración tiene lugar en la cima del Campanile de la plaza de San Marco. Los espectadores quedan entusiasmados: ante sus ojos, Murano, situado a 2 km y medio, parece estar a 300 m solamente.[cita requerida]
Galileo ofrece su instrumento y lega los derechos a la República de Venecia, muy interesada por las aplicaciones militares del objeto. En recompensa, es confirmado de por vida en su puesto de Padua y sus emolumentos se duplican. Se libera por fin de las dificultades financieras.[cita requerida]
Sin embargo, contrario a sus alegaciones, no dominaba la teoría óptica y los instrumentos fabricados por él son de calidad muy variable. Algunos telescopios son prácticamente inutilizables (al menos en observación astronómica). En abril de 1610, en Bolonia, por ejemplo, la demostración del telescopio es desastrosa, como así lo informa Martin Horky en una carta a Kepler.[cita requerida]
Galileo reconoció en marzo de 1610 que, entre más de 60 telescopios que había construido, solamente algunos eran adecuados. Numerosos testimonios, incluido el de Kepler, confirman la mediocridad de los primeros instrumentos.[cita requerida]
Observación de la Luna
Durante el otoño, Galileo continuó desarrollando su telescopio. En noviembre, fabrica un instrumento que aumenta veinte veces. Emplea tiempo para volver su telescopio hacia el cielo. Rápidamente, observando las fases de la Luna, descubre que este astro no es perfecto como lo quería la teoría aristotélica. La física aristotélica, que poseía autoridad en esa época, distinguía dos mundos:
- el mundo «sublunar», que comprende la Tierra y todo lo que se encuentra entre la Tierra y la Luna; en este mundo todo es imperfecto y cambiante;
- el mundo «supralunar», que comienza en la Luna y se extiende más allá. En esta zona, no existen más que formas geométricas perfectas (esferas) y movimientos regulares inmutables (circulares).
Galileo, por su parte, observó una zona transitoria entre la sombra y la luz, el terminador, que no era para nada regular, lo que por consiguiente invalidaba la teoría aristotélica y afirma la existencia de montañas en la Luna. Galileo incluso estima su altura en 7000 metros, más que la montaña más alta conocida en la época. Hay que decir que los medios técnicos de la época no permitían conocer la altitud de las montañas terrestres sin fantasías.[cita requerida] Cuando Galileo publica su Sidereus nuncius piensa que las montañas lunares son más elevadas que las de la Tierra, si bien en realidad son equivalentes.
Los enemigos de Galileo y la denuncia ante el Santo Oficio]
La oposición se organiza
Galileo parece ir de triunfo en triunfo y convence a todo el mundo. Por tanto, los partidarios de la teoría geocéntrica se convierten en enemigos encarnizados y los ataques contra él comienzan con la aparición de Sidereus nuncius. Ellos no pueden permitirse el perder la afrenta y no quieren ver su ciencia puesta en cuestión.
Además, los métodos de Galileo, basados en la observación y la experiencia en vez de la autoridad de los partidarios de las teorías geocéntricas (que se apoyan sobre el prestigio de Aristóteles), están en oposición completa con los suyos, hasta tal punto que Galileo rechaza compararse con ellos.
Al principio, solo se tratan de escaramuzas. Pero Sagredo escribe a Galileo, recién llegado a Florencia: «El poder y la generosidad de vuestro príncipe [el duque de Toscana] permiten esperar que él sepa reconocer vuestra dedicación y vuestro mérito; pero en los mares agitados actuales, ¿quién puede evitar de ser, yo no diría hundido, pero sí al menos duramente agitado por los vientos furiosos de los celos?».[cita requerida]
La primera flecha viene de Martin Horky, discípulo del profesor Magini y enemigo de Galileo. Este asistente publica en junio de 1610, sin consultar a su maestro, un panfleto contra el Sidereus nuncius. Exceptuando los ataques personales, su argumento principal es el siguiente: «Los astrólogos han hecho sus horóscopos teniendo en cuenta todo aquello que se mueve en los cielos. Por lo tanto los astros mediceos no sirven para nada y, Dios no crea cosas inútiles, estos astros no pueden existir».[cita requerida]
Horky es ridiculizado por los seguidores de Galileo, que responden que estos astros sirven para una cosa: hacerle enfadar. Convertido en el hazmerreír de la universidad, Horky finalmente es recriminado por su maestro: Magini no tolera un fallo tan claro. En el mes de agosto, un tal Sizzi intenta el mismo tipo de ataque con el mismo género de argumentos, sin ningún éxito.
Una vez que las observaciones de Galileo fueron confirmadas por el Colegio Romano, los ataques cambiaron de naturaleza. Ludovico delle Colombeataca sobre el plan religioso y se pregunta si Galileo cuenta con interpretar la Biblia para ponerla de acuerdo con sus teorías. En esta época en efecto, antes de los trabajos exegéticos del siglo XIX, un salmo (Salmo 93:1) da a entender una cosmología geocéntrica (dentro de la línea: «Tú has fijado la Tierra firme e inmóvil»)[cita requerida].
El cardenal Belarmino, que hizo quemar a Giordano Bruno, ordena que la Inquisición realice una investigación discreta sobre Galileo a partir de junio de 1611.
Los ataques se hacen más violentos
Galileo, de retorno a Florencia, es inatacable desde el punto de vista astronómico. Sus adversarios van entonces a criticar su teoría de los cuerpos flotantes. Galileo pretende que el hielo flota porque es más ligero que el agua, mientras que los aristotélicos piensan que flota porque es de su naturaleza el flotar (física cuantitativa y matemática de Galileo contra física cualitativa de Aristóteles). El ataque tendrá lugar durante un almuerzo en la mesa de Cosme II en el mes de septiembre de 1611.
Galileo se opone a los profesores de Pisa y en especial al mismo Delle Combe, durante lo que se denomina la «batalla de los cuerpos flotantes». Galileo sale victorioso del intercambio. Varios meses más tarde, sacará una obra en la que se presentará su teoría.
Además de estos asuntos, Galileo continúa con sus investigaciones. Su sistema de determinación de longitudes es propuesto en España por el embajador de Toscana.
En 1612, emprende una discusión con Apelles Latens Post Tabulam (seudónimo del jesuita Christoph Scheiner), un astrónomo alemán, sobre el tema de las manchas solares. Apelles defiende la incorruptibilidad del Sol argumentando que las manchas son en realidad conjuntos de estrellas entre el Sol y la Tierra. Galileo demuestra que las manchas están sobre la superficie misma del Sol, o tan próximas que no se puede medir su altitud. La Academia de los Lincespublicará esta correspondencia el 22 de marzo de 1613 con el título de Istoria e dimostrazioni intorno alle marchie solari e loro accidenti. Scheiner terminará por adherirse a la tesis galileana.
El 2 de noviembre de 1612, las querellas reaparecen. El dominico Niccolo Lorini, profesor de historia eclesiástica en Florencia, pronuncia un sermón resueltamente opuesto a la teoría de la rotación de la Tierra. Sermón sin consecuencias particulares, pero que marca los comienzos de los ataques religiosos. Los opositores utilizan el pasaje bíblico en el Libro de Josué (Josué 10:12-14) en el cual Josué detiene el movimiento del Sol y de la Luna, como arma teológica contra Galileo.
En diciembre de 1613, el profesor Benedetto Castelli, antiguo alumno de Galileo y uno de sus colegas en Pisa, es encargado por la duquesa Cristina de Lorena de probar la ortodoxia de la doctrina copernicana. Galileo vendrá en ayuda de su discípulo escribiéndole una carta el 21 de diciembre de 1613 (traducida como Galileo, diálogos y cartas selectas) sobre la relación entre ciencia y religión. La gran duquesa se tranquiliza, pero la controversia no se debilita.
Galileo mientras tanto continúa con sus trabajos. Del 12 al 15 de noviembre, recibe a Jean Tarde, a quien presenta su microscopio y sus trabajos de astronomía.
El 20 de diciembre, el padre Caccini ataca muy violentamente a Galileo en la iglesia Santa Maria Novella. El 6 de enero de 1614 un copernicano, el carmelita Paolo Foscarini, publica una carta tratando positivamente la opinión de los pitagóricos y de Copérnico sobre la movilidad de la Tierra. Él percibe el sistema copernicano como una realidad física. La controversia toma una amplitud tal que el cardenal Belarmino debe intervenir el 12 de abril. Éste escribe una carta a Foscarini donde condena sin equívocos la tesis heliocéntrica en ausencia de refutación concluyente del sistema geocéntrico. En dicha carta escribe:
Y no se puede responder que esto no es materia de fe, porque si no es materia de fe ex parti obiecti (respecto al objeto) es materia de fe ex parte dicentis (por quien lo dice). Y tan herético sería como quien dijera que Abraham no tuvo dos hijos y Jacob doce, o quien dijera que Cristo no nació de Virgen. — Cardenal Belarmino, «Carta a Foscarini». Opere XII, pp. 171–172.27
En 1614, conoce a Juan Bautista Baliani, físico genovés, que será su amigo y correspondiente durante largos años.
Como reacción, Galileo escribe a Cristina de Lorena una carta extensa en la cual desarrolla admirablemente sus argumentos en favor de la ortodoxia del sistema copernicano. Esta carta es, también, muy difundida. Esta carta, escrita hacia abril de 1615, es una pieza esencial del dossier. Ahí se ven los pasajes de las escrituras que poseen problemas desde un punto de vista cosmológico.
A pesar de ello, Galileo es obligado a presentarse en Roma para defenderse contra las calumnias y sobre todo para tratar de evitar una prohibición de la doctrina copernicana. Pero le falta la prueba irrefutable de la rotación de la Tierra para apoyar sus requerimientos. Su intervención llega demasiado tarde: Lorini, por carta de denuncia, ya había avisado a Roma de la llegada de Galileo y el Santo Oficio ya había comenzado la instrucción del caso.
El 8 de febrero de 1616, Galileo envía su teoría de las mareas (Discorso del flusso e reflusso) al cardenal Orsini. Esta teoría (a la cual se le ha reprochado durante mucho tiempo de estar en contradicción con el principio de la inercia enunciado por el mismo Galileo, y que sólo puede explicar pequeños componentes del fenómeno) pretendía demostrar que el movimiento de la Tierra producía las mareas, mientras que los astrónomos jesuitas ya postulaban con acierto que las mareas eran producidas por la atracción de la Luna.
MRUV
En este tipo de movimiento a diferencia del MRU (movimiento rectilíneo uniforme), la velocidadvaría. Pero esta variación a su vez es con un cierto orden, es decir que cambia un mismo intervalo en una misma cantidad de tiempo.
Por este hecho aparece una nueva magnitud llamada aceleración. La aceleración está representada por la fórmula:
a = (Vf – Vi) / T
La a es la aceleración, Vi es la velocidad del inicio y Vf es la velocidad final.
Para calcular la distancia recorrida se usa la siguiente fórmula:
D = Vi . T +/- ½ . a . T2
El signo positivo del segundo miembro se usa cuando el movimiento experimenta un aumento en su velocidad. Es una aceleración positiva. El signo menos se usa en situaciones de descenso de lavelocidad, o sea una aceleración negativa. Aquí vemos otra diferencia con respecto al MRU en el cual la distancia se calcula de forma mucho más sencilla.
Con respecto a los gráficos, también veremos otros distintos.
La gráfica de la distancia en función del tiempo tiene una forma parabólica. Esto es porque en la formula de la distancia podemos observar que la relación entre la distancia y el tiempo es cuadrática, o sea, responde a una función cuadrática. Cuando se tienen valores reales es importante colocar la unidad de cada magnitud. Para la distancia por ejemplo en metros y para el tiempo en segundos.
Cuando graficamos la velocidad versus el tiempo observaremos que esta relación corresponde a una función lineal. Ya que se arma a partir de la fórmula de aceleración. La velocidad puede expresarse en mts/seg o Km/h y el tiempo en horas o en segundos.
El último gráfico es la relación entre la aceleración y el tiempo. Para entenderlo mejor se grafica un ejemplo con valores. La a se expresa en mts/seg2 y el tiempo en seg. Se ve que un móvil que posee una a de 2 mts/seg2 y luego de un tiempo frena cambiando a una a negativa de por ejemplo 3 mts/seg2.
Problemas:
Calcula la distancia recorrida por un móvil que parte de reposo y alcanza una velocidad de 52 Km/h en 5 segundos.
Usaremos la formula:
D = Vi . T +/- ½ . a . T2
Tenemos como datos la velocidad final y el tiempo. Como el móvil parte del reposo su velocidad inicial es 0, por lo tanto el primer termino se anula.
D = + ½ . a . T2
El signo de la aceleración queda positivo ya que la velocidad aumenta de 0 al valor final de 52 Km/h.
La aceleración no la tenemos pero la podemos calcular. Para esto será conveniente previamente pasar la unidad de velocidad de Km/h a mts/seg para que sea compatible con el tiempo que est expresado en segundos.
Ahora procedemos a calcular la aceleración:
D = + ½ . 2,89 mts/seg2 . (5 seg)2
D = 36.125 mts.
Calcula la velocidad final de un móvil que viajando a una velocidad de 22 mts/seg acelera a razón de 2 mts/seg2 en 4 seg.
De la formula de aceleración hay que despejar la velocidad final.
a = (Vf – Vi) / T
Vf = a x T + Vi
Vf = 2 mts/seg2 x 4 seg + 22 mts/seg
Vf = 30 mts/seg
FORMULAS DE MRUV
a= v - vo v= vo + a*t t= v - vo
T a
s= vo*t + a*tcuadrdo vo= v - a*t 2as= v2 - vo2
2
s= (v + vo)*t a= v2 - vo2
2 2s
vf = velocidad final
vo = velocidad inicial
a = aceleración
t = tiempo
e = espacio o distancia
vo = velocidad inicial
a = aceleración
t = tiempo
e = espacio o distancia
CAÍDA LIBRE DE LOS CUERPOS
El movimiento de los cuerpos en caída libre (por la acción de su propio peso) es una forma derectilíneo uniformemente acelerado.
La distancia recorrida (d) se mide sobre la vertical y corresponde, por tanto, a una altura que se representa por la letra h.
En el vacío el movimiento de caída es de aceleración constante, siendo dicha aceleración la misma para todos los cuerpos, independientemente de cuales sean su forma y su peso.
La presencia de aire frena ese movimiento de caída y la aceleración pasa a depender entonces de la forma del cuerpo. No obstante, para cuerpos aproximadamente esféricos, la influencia del medio sobre el movimiento puede despreciarse y tratarse, en una primera aproximación, como si fuera de caída libre.
La aceleración en los movimientos de caída libre, conocida como aceleración de la gravedad, se representa por la letra g y toma un valor aproximado de 9,81 m/s2 (algunos usan solo el valor 9,8 o redondean en 10).
Si el movimiento considerado es de descenso o de caída, el valor de g resulta positivo como corresponde a una auténtica aceleración. Si, por el contrario, es de ascenso en vertical el valor de g se considera negativo, pues se trata, en tal caso, de un movimiento acelerado.
FORMULAS DE CAÍDA LIBRE:
1) v= vo + gt 6) 2gs= v al cuadado - vo al cuadrado
2) vo= v + gt 7) h= (v - vo) * t
3) v= vo al cuadrado + 2gY 2
4) h= vo*t + gt al cuadrado 8) v al cuadrado = vo al cuadrado = 2gh
2
5) t= v - vo
g
Problemas
1) Un policia hace un disparo hacia arriba verticalmente si la bala sale disparada con 300 mt/seg ¿cuak es la altura maxima que va hacendera? ¿Cual es el tiempo de su vida?
v= vo al cuadrado + 2gy
v= 300 mt/seg al cuadrado + 2(-9.8 mt/seg)
v= 300.03 mt/seg
t= v - vo
g
t= 300.03 mt/seg - 300 seg
9.8 mt/seg
t= 3.06 seg.
2) Desde lo alto de un edificio se suelta un objeto que tarda 3,5 seg en llegar al suelo. cuantos pies mide el edificio.
h= vo*t + gt al cuadrado
2
h= 0*3.5 seg + (32.2 pies/seg) * (3.5 seg)2
2
h= 197.22 pies.
3) Que altura a caido y con que velocidad fue lanzado hacia abajo un cuerpo que en 10 seg alquiere una velocidad de 11,800 cm/seg.
11,800 cm/seg*1mt = 110 mt/seg
100 cm
vo= v +gt
vo= 110 + (9.8)*(10)
vo= 208 mt/seg
h= (v -vo)*t
2
h= (110 - 208)*10
2
h= 490 mt.
3) Que altura a caido y con que velocidad fue lanzado hacia abajo un cuerpo que en 10 seg alquiere una velocidad de 11,800 cm/seg.
11,800 cm/seg*1mt = 110 mt/seg
100 cm
vo= v +gt
vo= 110 + (9.8)*(10)
vo= 208 mt/seg
h= (v -vo)*t
2
h= (110 - 208)*10
2
h= 490 mt.







ñiygdtr5tse4
ResponderEliminarEste comentario ha sido eliminado por el autor.
ResponderEliminarCasino Slot Machines - Casino Poker Software for Real Money
ResponderEliminarThe casino club w88 software from 슬롯 사이트 the gambling 실시간 배팅 사이트 industry offers casino slots, table games, video poker, bingo, bingo 마추 자 먹튀 and video poker. 맥스 벳